Note
Go to the end to download the full example code.
Extracting and processing LISN data for Cartolabe (LDA projection)¶
In this example we will:
extract entities (authors, articles, labs, words) from a collection of scientific articles
project those entities in 2 dimensions
cluster them
find their nearest neighbors.
Download data¶
We will first download the CSV file that contains all articles from HAL (https://hal.archives-ouvertes.fr/) published by authors from LISN (Laboratoire Interdisciplinaire des Sciences du Numérique) between 2000-2022.
from download import download
csv_url = "https://zenodo.org/record/7323538/files/lisn_2000_2022.csv"
download(csv_url, "../datas/lisn_2000_2022.csv", kind='file',
progressbar=True, replace=False)
Downloading data from https://zenodo.org/records/7323538/files/lisn_2000_2022.csv (6.3 MB)
file_sizes: 0%| | 0.00/6.59M [00:00<?, ?B/s]
file_sizes: 39%|██████████▏ | 2.59M/6.59M [00:00<00:00, 25.3MB/s]
file_sizes: 100%|██████████████████████████| 6.59M/6.59M [00:00<00:00, 44.2MB/s]
Successfully downloaded file to ../datas/lisn_2000_2022.csv
'../datas/lisn_2000_2022.csv'
Load data to dataframe¶
import pandas as pd # noqa
df = pd.read_csv('../datas/lisn_2000_2022.csv', index_col=0)
df.head()
The dataframe that we just read consists of 4262 articles as rows.
print(df.shape[0])
4262
And their authors, abstract, keywords, title, research labs and domain as columns.
print(*df.columns, sep="\n")
structId_i
authFullName_s
en_abstract_s
en_keyword_s
en_title_s
structAcronym_s
producedDateY_i
producedDateM_i
halId_s
docid
en_domainAllCodeLabel_fs
Creating correspondance matrices for each entity type¶
From this table of articles, we want to extract matrices that will map the correspondance between these articles and the entities we want to use.
Labs¶
Similarly, we can create matrices for the labs by simply passing the structAcronym_s column to the function.
labs_mat, labs_scores = load_comma_separated_column(df,
'structAcronym_s',
filter_acronyms=True)
labs_scores.head()
LRI 4789
UP11 6271
CNRS 10217
LISN 5203
LMS 1
dtype: int64
Checking the number of columns of the sparse matrix labs_mat, we see that there are 1818 distict labs.
labs_mat.shape[1]
1818
Filtering low score entities¶
A lot of the authors and labs that we just extracted from the dataframe have a very low score, which means they’re only linked to one or two articles. To improve the quality of our data, we’ll filter the authors and labs by removing those that appear less than 4 times.
To do this, we’ll use the filter_min_score function.
from cartodata.operations import filter_min_score # noqa
authors_before = len(authors_scores)
labs_before = len(labs_scores)
authors_mat, authors_scores = filter_min_score(authors_mat,
authors_scores,
4)
labs_mat, labs_scores = filter_min_score(labs_mat,
labs_scores,
4)
print(f"Removed {authors_before - len(authors_scores)} authors with less "
f"than 4 articles from a total of {authors_before} authors.")
print(f"Working with {len(authors_scores)} authors.\n")
print(f"Removed {labs_before - len(labs_scores)} labs with less than "
f"4 articles from a total of {labs_before}.")
print(f"Working with {len(labs_scores)} labs.")
Removed 6654 authors with less than 4 articles from a total of 7348 authors.
Working with 694 authors.
Removed 1255 labs with less than 4 articles from a total of 1818.
Working with 563 labs.
Words¶
For the words, it’s a bit trickier because we want to extract n-grams (groups of n terms) instead of just comma separated values. We’ll call the load_text_column which uses scikit-learn’s CountVectorizer to create a vocabulary and map the tokens.
from cartodata.loading import load_text_column # noqa
from sklearn.feature_extraction import text as sktxt # noqa
with open('../datas/stopwords.txt', 'r') as stop_file:
stopwords = sktxt.ENGLISH_STOP_WORDS.union(
set(stop_file.read().splitlines()))
df['text'] = df['en_abstract_s'] + ' ' \
+ df['en_keyword_s'].astype(str) + ' ' \
+ df['en_title_s'].astype(str) + ' ' \
+ df['en_domainAllCodeLabel_fs'].astype(str)
words_mat, words_scores = load_text_column(df['text'],
4,
10,
0.05,
stopwords=stopwords)
Here words_scores contains a list of all the n-grams extracted from the documents with their score,
words_scores.head()
abilities 21
ability 164
absence 53
absolute 19
abstract 174
dtype: int64
and the words_mat matrix counts the occurences of each of the 4282 n-grams for all the articles.
words_mat.shape
(4262, 4682)
To get a better representation of the importance of each term, we’ll also apply a TF-IDF (term-frequency times inverse document-frequency) normalization on the matrix.
The normalize_tfidf simply calls scikit-learn’s TfidfTransformer class.
from cartodata.operations import normalize_tfidf # noqa
words_mat = normalize_tfidf(words_mat)
Articles¶
Finally, we need to create a matrix that simply maps each article to itself.
from cartodata.loading import load_identity_column # noqa
articles_mat, articles_scores = load_identity_column(df, 'en_title_s')
articles_scores.head()
Termination and Confluence of Higher-Order Rewrite Systems 1.0
Efficient Self-stabilization 1.0
Resource-bounded relational reasoning: induction and deduction through stochastic matching 1.0
Reasoning about generalized intervals : Horn representability and tractability 1.0
Proof Nets and Explicit Substitutions 1.0
dtype: float64
Dimension reduction¶
One way to see the matrices that we created is as coordinates in the space of all articles. What we want to do is to reduce the dimension of this space to make it easier to work with and see.
LDA projection¶
We use LDA (Latent Dirichlet Allocation) technique to identify keywords in our data and thus reduce the number of rows in our matrices. The lda_projection method takes three arguments:
the number of dimensions you want to keep
the id of the documents/words matrix in the 3rd parameter list
a list of matrices to project
It returns a list of the same length containing the matrices projected in the latent space.
We also apply an l2 normalization to each feature of the projected matrices.
from cartodata.projection import lda_projection # noqa
from cartodata.operations import normalize_l2 # noqa
lda_matrices = lda_projection(50,
2,
[articles_mat, authors_mat, words_mat, labs_mat])
lda_matrices = list(map(normalize_l2, lda_matrices))
We’ve reduced the number of rows in each of articles_mat, authors_mat, words_mat and labs_mat to just 50.
print(f"articles_mat: {lda_matrices[0].shape}")
print(f"authors_mat: {lda_matrices[1].shape}")
print(f"words_mat: {lda_matrices[2].shape}")
print(f"labs_mat: {lda_matrices[3].shape}")
articles_mat: (50, 4262)
authors_mat: (50, 694)
words_mat: (50, 4682)
labs_mat: (50, 563)
This makes it easier to work with them for clustering or nearest neighbors tasks, but we also want to project them on a 2D space to be able to map them.
UMAP projection¶
The UMAP (Uniform Manifold Approximation and Projection) is a dimension reduction technique that can be used for visualisation similarly to t-SNE.
We use this algorithm to project our matrices in 2 dimensions.
from cartodata.projection import umap_projection # noqa
umap_matrices = umap_projection(lda_matrices)
Now that we have 2D coordinates for our points, we can try to plot them to get a feel of the data’s shape.
import matplotlib.pyplot as plt # noqa
import numpy as np # noqa
import seaborn as sns # noqa
# %matplotlib inline
sns.set(style='white', rc={'figure.figsize': (12, 8)})
labels = ('article', "auth", "words", "labs")
colors = ['g', 'r', 'b', 'y']
markers = ['o', 's', '+', 'x']
def plot(matrices):
plt.close('all')
fig, ax = plt.subplots()
axes = []
for i, m in enumerate(matrices):
axes.append(ax.scatter(m[0, :], m[1, :],
color=colors[i], marker=markers[i],
label = labels[i]))
leg = ax.legend((axes[0], axes[1], axes[2], axes[3]),
labels,
fancybox=True, shadow=True)
return fig, ax
fig, ax = plot(umap_matrices)
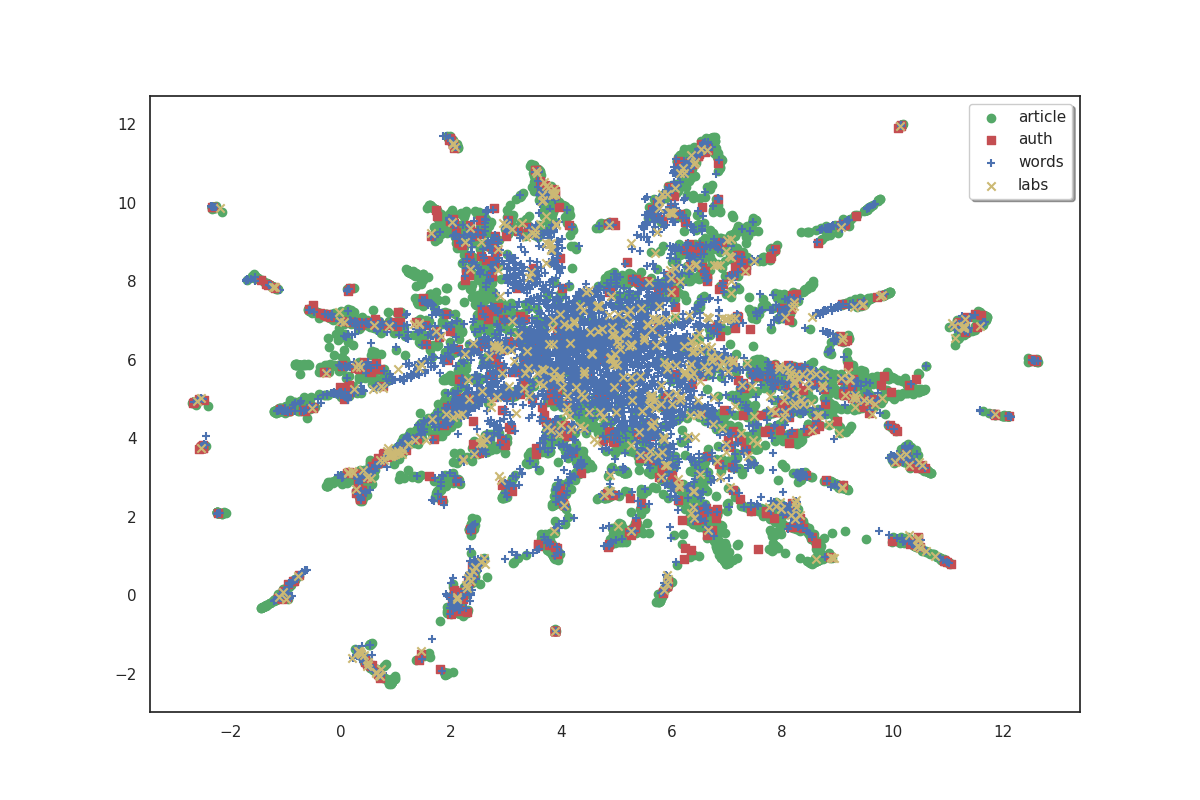
On the plot above, articles are shown in green, authors in red, words in blue and labs in yellow. Because we don’t have labels for the points, it doesn’t make much sense as is. But we can see that the data shows some clusters which we could try to identify.
Clustering¶
In order to identify clusters, we use the KMeans clustering technique on the articles. We’ll also try to label these clusters by selecting the most frequent words that appear in each cluster’s articles.
from cartodata.clustering import create_kmeans_clusters # noqa
cluster_labels = []
c_lda, c_umap, c_scores, c_knn, _, _, _ = create_kmeans_clusters(8, # number of clusters to create
# 2D matrix of articles
umap_matrices[0],
# the 2D matrix of words
umap_matrices[2],
# the articles to words matrix
words_mat,
# word scores
words_scores,
# a list of initial cluster labels
cluster_labels,
# LDA space matrix of words
lda_matrices[2])
c_scores
""
fig, ax = plot(umap_matrices)
for i in range(8):
ax.annotate(c_scores.index[i], (c_umap[0, i], c_umap[1, i]),
color='red')
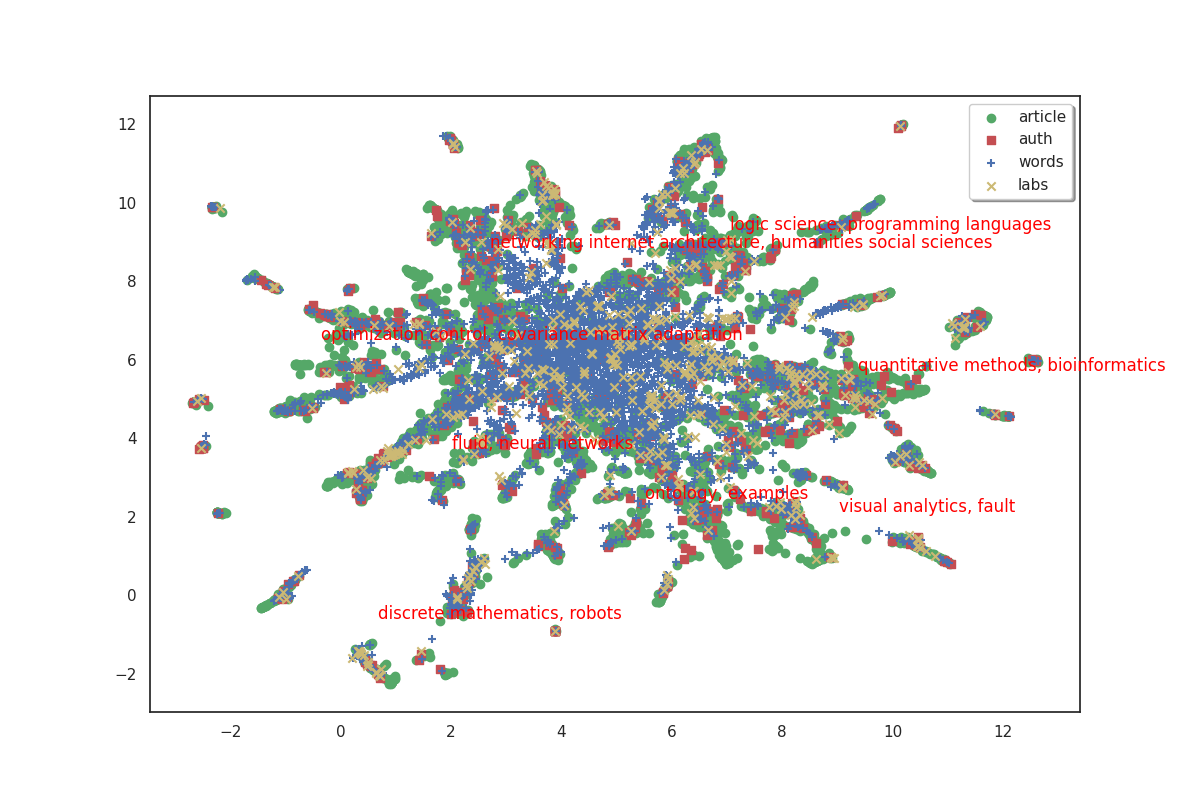
The 8 clusters that we created give us a general idea of what the big clusters of data contain. But we’ll probably want a finer level of detail if we start to zoom in and focus on smaller areas. So we’ll also create a second bigger group of clusters. To do this, simply increase the number of clusters we want.
mc_lda, mc_umap, mc_scores, mc_knn, _, _, _ = create_kmeans_clusters(32,
umap_matrices[0],
umap_matrices[2],
words_mat,
words_scores,
cluster_labels,
lda_matrices[2])
mc_scores
fault tolerant, fault tolerance 72
discrete event systems, touch 262
approximate bayesian, adjacency 88
evolutionary robotics, deductive program verification 157
natural language processing, reinforcement learning 153
means, architectures 101
verification, floating point 152
belief propagation, number searchers 76
black optimization, distributed algorithm 86
documents, ontologies 251
internet architecture, wireless networks 177
genomes, materialized views 161
adaptation, displays 202
cognitive, visualization techniques 130
compiler, automata 226
tangible, modulo 174
mobile robots, lower bounds 100
computational complexity, population protocols 82
numerical simulations, fluid mechanics 113
large scale, sequences 106
neural evolutionary computing, large hadron collider 80
analytics, social networks 196
social sciences, internet 180
cloud radio access networks, cloud radio access network 24
metabolic, ontology alignment 92
regulatory network, gesture 49
secondary structures, cloud computing 196
challenge, matter 182
monte carlo search, black 110
interfaces, supported 131
molecular biology, protein protein 63
query, semantics 90
dtype: int64
Nearest neighbors¶
One more thing which could be useful to appreciate the quality of our data would be to get each point’s nearest neighbors. If our data processing is done correctly, we expect the related articles, labs, words and authors to be located close to each other.
Finding nearest neighbors is a common task with various algorithms aiming to solve it. The get_neighbors method uses one of these algorithms to find the nearest points of each type. It takes an optional weight parameter to tweak the distance calculation to select points that have a higher score but are maybe a bit farther instead of just selecting the closest neighbors.
Because we want to find the neighbors of each type (articles, authors, words, labs) for all of the entities, we call the get_neighbors method in a loop and store its results in an array.
from cartodata.neighbors import get_neighbors # noqa
scores = [articles_scores, authors_scores, words_scores, labs_scores]
weights = [0, 0.5, 0.5, 0]
all_neighbors = []
for idx in range(len(lda_matrices)):
all_neighbors.append(get_neighbors(lda_matrices[idx],
scores[idx],
lda_matrices,
weights[idx]))
Exporting¶
We now have sufficient data to create a meaningfull visualization.
from cartodata.operations import export_to_json # noqa
natures = ['articles',
'authors',
'words',
'labs',
'hl_clusters',
'ml_clusters'
]
export_file = '../datas/lisn_workflow_lda.json'
# add the clusters to list of 2d matrices and scores
matrices = list(umap_matrices)
matrices.extend([c_umap, mc_umap])
scores.extend([c_scores, mc_scores])
# Create a json export file with all the infos
export_to_json(natures,
matrices,
scores,
export_file,
neighbors_natures=natures[:4],
neighbors=all_neighbors)
This creates the lisn_workflow_lda.json file which contains a list of points ready to be imported into Cartolabe. Have a look at it to check that it contains everything.
import json # noqa
with open(export_file, 'r') as f:
data = json.load(f)
data[1]['position']
[2.274456024169922, 9.282912254333496]
Total running time of the script: (2 minutes 0.487 seconds)